基本概念
布隆过滤器(英语:Bloom Filter)是 1970 年由布隆提出,是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。 它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。 – 维基百科
查找问题建模
如何判断某个元素是否存在于一个集合中?
比较直观的做法是将所有元素保存起来,然后逐个比较确认结果,建模转换为具体的数据结构:
- 线性结构: 数组、链表等,时间复杂度为 O(N), 空间复杂度为 O(N)
- 散列表结构: Map、HashTable 等, 时间复杂度为 O(1), 空间复杂度为 O(N)
- 树形结构: AVL、RBTree 等, 时间复杂度为 O(logN), 空间复杂度为 O(N)
常见的数据结构随着元素的增加,存储空间也会越来越大,同时查询速度也会越来越慢 (散列表结构不受影响),如果我们希望在保持时间复杂度为 O(N) 的前提下, 尽可能地降低内存占用,就需要转换一下思路:保存特征数据,而非所有数据。什么是特征数据? 简单来说,就是能够唯一标识出其对应的源数据, 比如常见的 用户 ID、游戏中奖 ID、管理后台审批流 ID 等。
原理和应用场景
布隆过滤器的原理: 当一个元素被加入集合时,通过 K 个哈希函数 将元素映射到一个位图数据结构 (例如 bitmap) 中的 K 个位置上面,并将这些位置全部置为 1。 判断元素是否存在于集合时,只需查看 K 个哈希函数 映射后的 K 个位置上面的值即可。
如果这些位置任意一个为 0,则表示被检测元素一定不存在于集合中,如果都是 1,则表示被检测元素有较大可能存在于集合中。
为什么不能检测 “一定存在” ?
检测元素时可以返回 “一定不存在” 和 “可能存在”,因为可能有多个元素映射到相同的 bit 上面,导致该位置为 1, 那么一个不存在的元素也可能会被误判为存在, 所以无法提供 “一定存在” 的语义保证。
为什么元素不允许被 “删除” ?
如果删除了某个元素,导致对应的 bit 位置为 0, 但是可能有多个元素映射到相同的 bit 上面,那么一个存在的元素会被误判为不存在 (这是不可接收的), 所以为了 “一定不存在” 的语义保证,元素不允许被删除。
PS: 虽然可以引入一个 删除计数器 来解决上述问题,不过这需要引入额外的空间,失去了使用过滤器的意义。
两个语义操作
- Add : 添加一个元素到集合中
- Test : 检查给定元素是否存在于集合中
示例
URL 去重
假设下面的 URL 列表为采集队列 (一共 100 条数据),我们希望采集完成的 URL 可以记录起来,避免多次采集,如果使用正常的字符串存储的话 (以 Go 语言为例,string 占用 16 bytes), 大概需要 16 bytes * 100 = 1600 bytes 内存空间。
https://www.example.com/u/101/profile
https://www.example.com/u/102/profile
...
https://www.example.com/u/200/profilehttps://www.example.com/u/101/profile
https://www.example.com/u/102/profile
...
https://www.example.com/u/200/profile而如果我们改为 布隆过滤器 的方式来记录的话,假设哈希函数可以将每个链接转换为 1 个 0-255 的数字,通过将数据存入一个 bitmap, 那么理想情况下 (不发生任何碰撞) 最终只需要 1 个 byte 的内存空间即可,内存使用直接降低了 1600 倍。
# 布隆过滤器记录 URL 只需要 1 个 byte
------------------------------------
| 0 | 1 | 2 | 3 | ... | 255 |
------------------------------------
| URL | URL | URL | | | URL |
------------------------------------# 布隆过滤器记录 URL 只需要 1 个 byte
------------------------------------
| 0 | 1 | 2 | 3 | ... | 255 |
------------------------------------
| URL | URL | URL | | | URL |
------------------------------------网站用户性别
假设网站的用户数量为 1000万,每个用户性别存储需要 1 个 bytes, 如果正常存储的话,大概需要 1 byte * 1000 W ≈ 10 MB 内存空间。
而如果我们改为 布隆过滤器 的方式来记录的话,假设用户 ID 是一个数字,通过将数据存入一个 bitmap, 那么 1 byte 可以表示 256 个 用户性别, 理想情况下 (不发生任何碰撞) 最终只需要 1000 W / 256 * 1 byte ≈ 0.04 MB 内存空间,内存使用直接降低了 256 倍。
# 布隆过滤器记录用户网站性别
--------------------------------------------------
| 0 | 1 | 2 | 3 | ... | 9999999 |
--------------------------------------------------
| User1 | User2 | User3 | User4 | ... | User... |
--------------------------------------------------# 布隆过滤器记录用户网站性别
--------------------------------------------------
| 0 | 1 | 2 | 3 | ... | 9999999 |
--------------------------------------------------
| User1 | User2 | User3 | User4 | ... | User... |
--------------------------------------------------其他应用场景
- 垃圾邮件过滤
- 防止缓存穿透
- 业务记录计数器
- Web 拦截
两个核心支撑点
通过上面两个简单的应用场景可以看到,要实现一个健壮的 布隆过滤器,需要规划设计好两个技术点:
- 元素长度和用于存储哈希映射值的数据结构,一般使用 bitmap (具体的长度和存储规模有关)
- 显著降低碰撞、性能优良的哈希函数
Murmur3,FNV 系列和 Jenkins 等非密码学算法适合作为哈希函数,其中 Murmur3 因为易于实现,并且在速度和随机分布上有很好的权衡, 实践中多选用其作为 布隆过滤器 的哈希函数。
数学部分
一个 布隆过滤器 至少需要包含如下参数:
- 哈希空间大小,记为
m - 元素集合大小,记为
n - 哈希函数个数,记为
k - 误判概率,记为
p(可能出现一个元素不在集合中,但是被误判为存在于集合中,这个误判的概率取值范围为0 - 1)
哈希函数个数满足以下公式时,布隆过滤器 有最好的效果 (数学证明部分省略,数学渣暴露了 😦 … )
k = [(ln2)(m/n)]
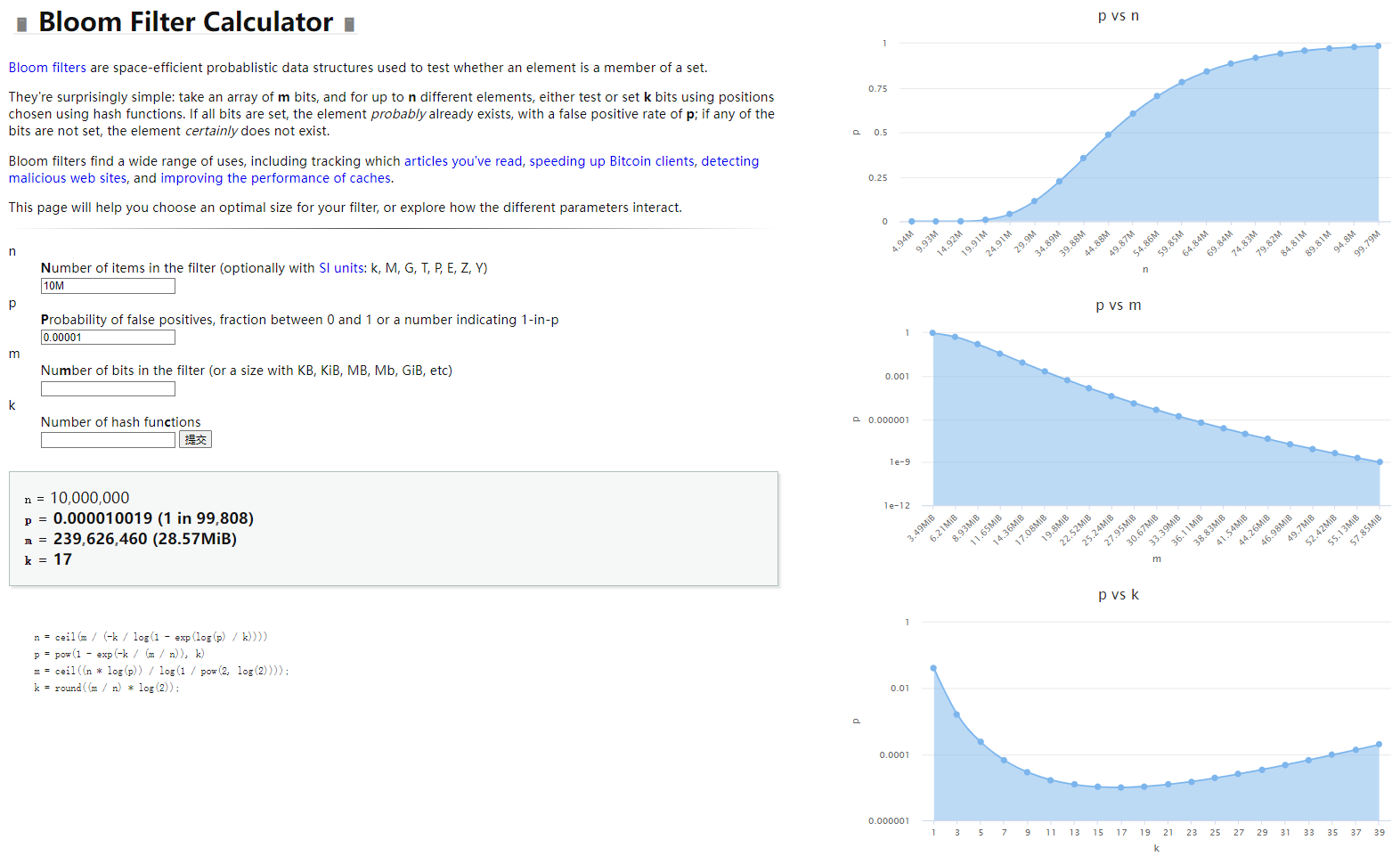
还是以刚才的 网站用户性别 为例,1000W 用户需要以不高于 0.00001% 误判率的的情况下被检测到,需要多少个哈希函数?需要耗费多少空间?
# 带入公式计算
n = ceil(m / (-k / log(1 - exp(log(p) / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))))
k = round((m / n) * log(2))# 带入公式计算
n = ceil(m / (-k / log(1 - exp(log(p) / k))))
p = pow(1 - exp(-k / (m / n)), k)
m = ceil((n * log(p)) / log(1 / pow(2, log(2))))
k = round((m / n) * log(2))记不住数学公式?没关系,已经有大佬做好了一个 在线工具,可以通过输入参数直接生成对应的哈希函数个数。
开源库
笔者选择了 bits-and-blooms/bloom 作为研究 布隆过滤器 代码实现,版本为 v3.3.1。
安装组件
$ go get -u github.com/bits-and-blooms/bloom/v3$ go get -u github.com/bits-and-blooms/bloom/v3示例
初始化过滤器时,需要知道对应的业务场景有多少元素(期望的容量),以及期望的误判概率。常见的误判率为 1%, 误报率越低,需要的内存就越多, 同时容量越大,需要的内存就越多。
初始化过滤器时,应该尽可能明确需要的元素数量,因为 布隆过滤器 不是动态数据结构,如果指定的元素数量太少,则可能会超出误判概率范围。
package main
import "github.com/bits-and-blooms/bloom"
func main() {
// 初始化能够接收 100 万个元素且误判率为 1% 的布隆过滤器
filter := bloom.NewWithEstimates(1000000, 0.01)
hw := []byte(`hello world`)
hg := []byte(`hello golang`)
filter.Add(hw)
println(filter.Test(hw)) // true
println(filter.Test(hg)) // false
}package main
import "github.com/bits-and-blooms/bloom"
func main() {
// 初始化能够接收 100 万个元素且误判率为 1% 的布隆过滤器
filter := bloom.NewWithEstimates(1000000, 0.01)
hw := []byte(`hello world`)
hg := []byte(`hello golang`)
filter.Add(hw)
println(filter.Test(hw)) // true
println(filter.Test(hg)) // false
}我们只添加了 hello world 字符串到过滤器中,所以正常的输出应该是 true false:
$ go run main.go
true
false$ go run main.go
true
false源码分析
接下来,我们来简单分析下 bits-and-blooms/bloom 的实现代码。
哈希算法选择
module github.com/bits-and-blooms/bloom/v3
go 1.14
require (
github.com/bits-and-blooms/bitset v1.3.1
github.com/twmb/murmur3 v1.1.6
)module github.com/bits-and-blooms/bloom/v3
go 1.14
require (
github.com/bits-and-blooms/bitset v1.3.1
github.com/twmb/murmur3 v1.1.6
)从 bits-and-blooms/bloom 的依赖包中,可以看到其选择了 murmur3 算法作为哈希函数实现。
BloomFilter
BloomFilter 结构体表示一个 布隆过滤器,包含 3 个字段,分别对应上文提到的 布隆过滤器 的必要参数。
type BloomFilter struct {
m uint // 哈希空间大小
k uint // 哈希函数个数
b *bitset.BitSet // bitmap
}type BloomFilter struct {
m uint // 哈希空间大小
k uint // 哈希函数个数
b *bitset.BitSet // bitmap
}初始化过滤器
NewWithEstimates 方法创建一个 布隆过滤器,内部调用了 EstimateParameters 方法来计算 m 和 k 的值, 最后通过 m 和 k 初始化一个 BloomFilter 结构体并返回。
func NewWithEstimates(n uint, fp float64) *BloomFilter {
m, k := EstimateParameters(n, fp)
return New(m, k)
}
func EstimateParameters(n uint, p float64) (m uint, k uint) {
m = uint(math.Ceil(-1 * float64(n) * math.Log(p) / math.Pow(math.Log(2), 2)))
k = uint(math.Ceil(math.Log(2) * float64(m) / float64(n)))
return
}func NewWithEstimates(n uint, fp float64) *BloomFilter {
m, k := EstimateParameters(n, fp)
return New(m, k)
}
func EstimateParameters(n uint, p float64) (m uint, k uint) {
m = uint(math.Ceil(-1 * float64(n) * math.Log(p) / math.Pow(math.Log(2), 2)))
k = uint(math.Ceil(math.Log(2) * float64(m) / float64(n)))
return
}添加元素
BloomFilter.Add 方法添加一个元素到 布隆过滤器,返回当前的 BloomFilter 对象来支持链式调用。
func (f *BloomFilter) Add(data []byte) *BloomFilter {
h := baseHashes(data)
for i := uint(0); i < f.k; i++ {
f.b.Set(f.location(h, i))
}
return f
}func (f *BloomFilter) Add(data []byte) *BloomFilter {
h := baseHashes(data)
for i := uint(0); i < f.k; i++ {
f.b.Set(f.location(h, i))
}
return f
}baseHashes 函数返回哈希函数计算出的哈希值,其内部调用了 murmur3 算法。
func baseHashes(data []byte) [4]uint64 {
...
}func baseHashes(data []byte) [4]uint64 {
...
}location 函数返回哈希值对应的 bitmap 的位置索引,通过将 bitmap 对应的位置进行设置,就可以将元素添加到 布隆过滤器 了。
func location(h [4]uint64, i uint) uint64 {
...
}func location(h [4]uint64, i uint) uint64 {
...
}检测元素
BloomFilter.Test 方法检测一个元素是否存在于 布隆过滤器 中,可以看到,其内部实现就是 BloomFilter.Add 方法的逆过程。
func (f *BloomFilter) Test(data []byte) bool {
h := baseHashes(data)
for i := uint(0); i < f.k; i++ {
if !f.b.Test(f.location(h, i)) {
return false
}
}
return true
}func (f *BloomFilter) Test(data []byte) bool {
h := baseHashes(data)
for i := uint(0); i < f.k; i++ {
if !f.b.Test(f.location(h, i)) {
return false
}
}
return true
}调用流程图
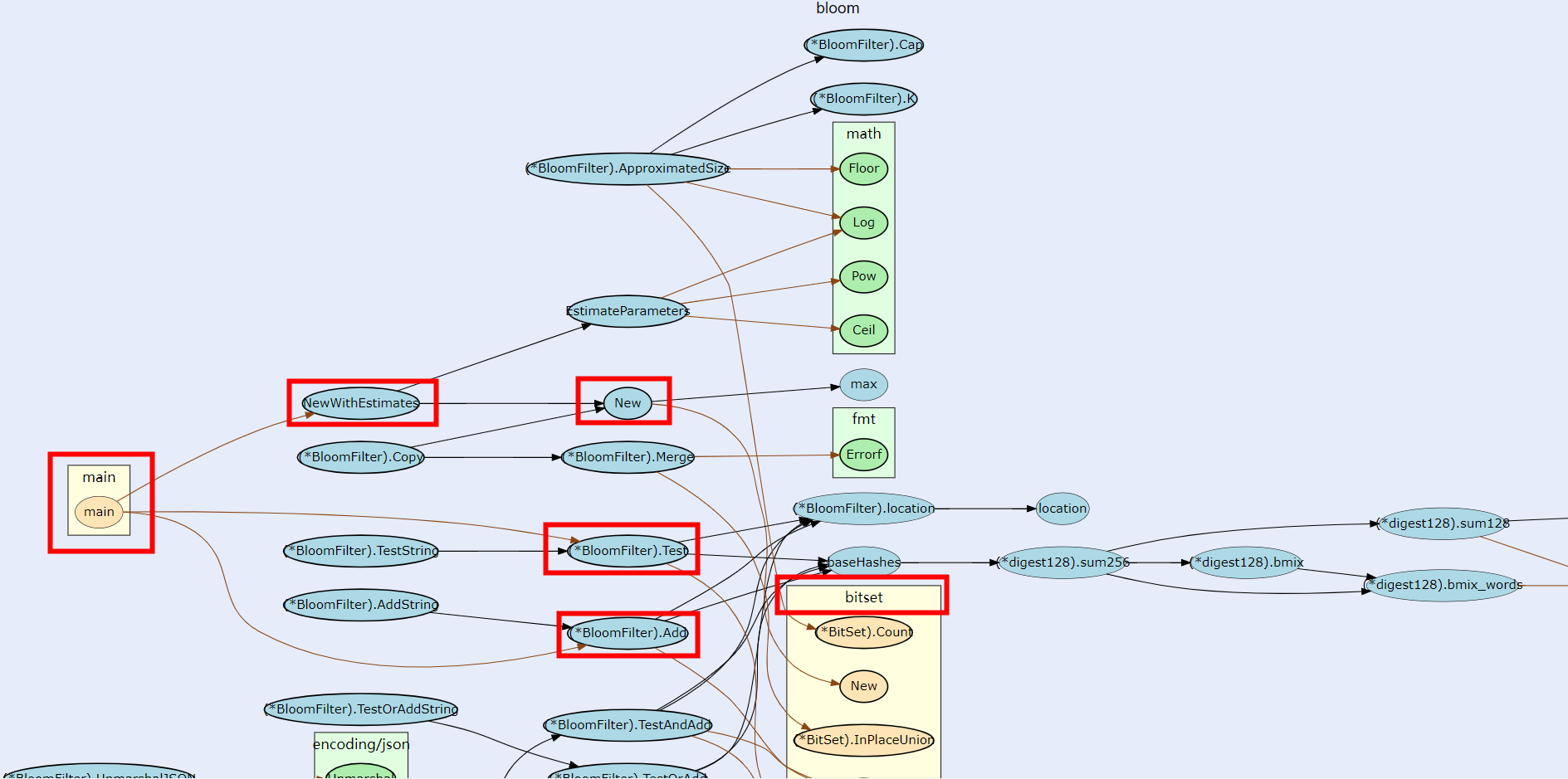
小结
本文简述了 布隆过滤器 的基本概念和原理,并通过开源库 bits-and-blooms/bloom 的实现代码分析了实现 布隆过滤器 的核心技术点, 最后引用维基百科关于 布隆过滤器 的优缺点作为文章结尾。
优点
布隆过滤器 在算法的空间复杂度和时间复杂度方面都有巨大的优势,Add 和 Test 操作的时间复杂度都是常数 O(K) (K: 哈希函数个数)。 由于哈希函数相互之间没有关联,因此可以通过硬件并行实现计算加速,此外,由于 布隆过滤器 不存储源数据,在某些对数据保密要求非常严格的场景 (数据可用,但不可见) 有明显优势。 最后,在哈希空间向量长度相同的情况下,使用同一组哈希函数的两个 布隆过滤器 的 集合相关运算可以使用位操作进行。
缺点
布隆过滤器 最明显的的缺点就是 误判率,随着元素数量增加,误判率 也随之增加,所以如果元素数量很少的情况下,使用 map 就可以了。 此外,布隆过滤器 不支持删除元素, 因为 布隆过滤器 只能确定元素一定不存在于集合中,无法确定元素一定存在于集合中,如果一定要删除某个元素, 则必须重新构建整个 布隆过滤器。